Some interesting optical properties of the human eye
In the previous section we saw that the eye is rather similar to a camera. It lets light in through an opening of variable diameter (the pupil) and lenses are used to form an inverted real image on the back of the eye (the retina). Unlike a camera refraction (i.e. bending of light) is accomplished by two structures: the front surface of the cornea and the eyelens. The corneal surface does most of the refraction, while changes in the shape of the eyelens fine tune the focus of the image.
Although focusing of the image by the eye involves two "lenses" it is possible to predict how the optics of the eye works quite effectively by modeling it as having a single convex lens. The average adult human eye is 2.4 cm from the front of the cornea to the back of the eye. We can model the optics of the eye by treating it as consisting of a single converging lens positioned 1.7 cm. from the back of the eye. This is pictured below.
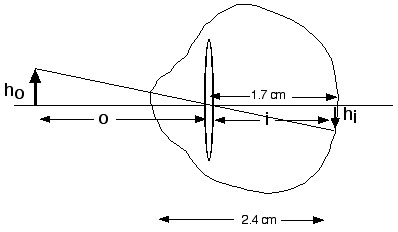
If the eye is functioning normally, when the eyelens is at rest (i.e. the ciliary muscles are relaxed and the eyelens is therefore stretched to a fairly flat shape) parallel rays striking the surface of the eye will be brought to focus at the retina. In other words at rest the focal length of the lens in the model eye is 1.7 cm.
For a simple optical system like that shown above it is easy to relate certain key quantities using an equation known as the simple lens equation. Note the quantities depicted in the picture below. The distance from object to the center of the lens is called the "object distance" or "o". The distance from the center of the lens to where the image is formed is called the image distance or "i". The focal length of the lens is "f". Finally the height of the object is referred to as "ho" and the height of the image is referred to as "hi". The lens equation tells us that
1/o + 1/i = 1/f
It is also possible to show that hi/ho
= -i/o
where a negative value refers to an inverted image. This value is also known
as the linear magnification.
This equation is illustrated at the following website:
Hyper Physics: Image Formation
These equations are very useful because if we know any two
pieces of information (e.g. the object distance and the focal length) we can
figure out the other values. On the web page described above there is a calculator
that lets you plug in values of two of the variables and calculate the others.
Alternatively one can do the fairly simple math to get the same answers.
IMAGE POSITION
Now let's use these equations to ask some questions about the eye. Suppose an individual can see distant objects perfectly but is unable to change the shape of the eyelens. What happens to the image as objects are moved closer to the eye. If the image is perfect for distant objects we know that the focal length of this lens system = 1.7 cm. We can now calculate the image distance (i.e. distance from center of the lens to the retina) for a series of object distances and we get the following answers:
* because rays diverging from the focal point
emerge from the lens as parallel rays
We can make a graph of the data as follows:
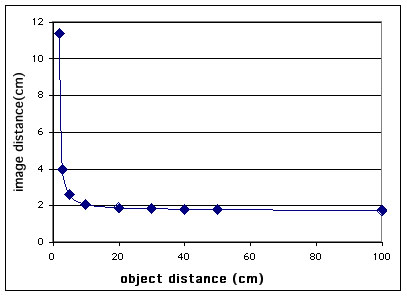
Notice that from infinity (i.e. beyond 10,000 cm) to 100 cm
object distance there is very little change in the image distance. Since the
eye has some depth of focus (see section on cameras -- the same phenomenon
occurs in the eye) there is very little need to adjust focus. However at distances
shorter than 100 cm object distance a great deal of adjustment will be needed
by the eyelens in order to keep the image focused on the retina.
In real life as humans age the eyelens loses its flexibility and the ability to adjust focus is lost. This generally has no effect on vision at a distance. There is only a problem at very close distances, and thus it is for reading that older people need glasses. Reading glasses are positive lenses which have the effect of decreasing the focal length of the eye optics. We say that decreasing the focal length of a lens represents an increase in its power -- it bends light more sharply. The reading glasses replace the normal rounding up of the lens that allows us to focus at close distances.
IMAGE SIZE
We can use the same approach to look
at how the size of the image on the retina changes.
Using our same model eye we can figure out that if the image and object distance
are the same, then the image and object are the same size. Since the a focused
image sits 1.7 cm from the center of the lens of the model eye, in order to
get our image and object to be equal in size the object should be 1.7 cm in
front of the model lens. Since the front of the eye in our model sits 0.7
cm in front of the lens, an object 1 cm in front of the cornea will give us
an image/object ratio of -1.0.
In class we used this calculation to allow us to measures the effect of object distance on image size. By placing a small ruler 1.0 cm in front of our eye we were in effect placing a equal-sized ruler on the retina. Then we measured an object of known size placed various distances from the eye. We could get the same result using our lens equation calculator.
However one does it, the results are similar to the graph shown below. In this case I have plotted the size of the image created by a 1 cm tall object on the retina as a function of distance. The numbers are negative to indicate that the image is inverted.
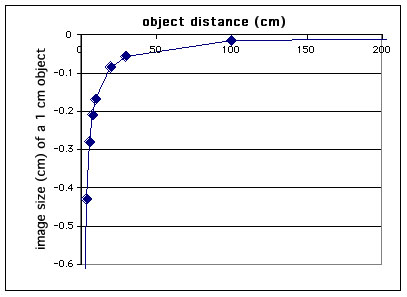
This shows us that images grow very quickly close to the eye, but the rate
of decrease of the image size slows dramatically as one goes further away
from the eye. It is actually fairly amazing that our brain can sort out the
change in an image's size with its distance away. This is accomplished by
analyzing the distance away an object is as well as its apparent size. The
main mechanism for estimating object distances in humans is to gauge how sharply
turned in the two eyes need to be in order to have both eyes look a the same
object. With one eye closed it is much harder to judge distance, although
experience with how objects changes size with distance and knowledge of the
size of objects in the visual field help the brain estimate distances as well.
OPTICAL IRREGULARITIES OF THE EYE
An eye that brings distant object to focus on the retina (i.e. a normal eye) is said to be emmetropic. When the eyeball is too long, such that objects are brought to focus in front of the retina the eye is said to be myopic, or near-sighted. When the eyeball is too short, so that the image of distance objects form behind the retina the eye is said to be hyperopic, or far-sighted. Eyes are often irregular in shape such that at some angles (e.g. horizontal) the eye brings the image to focus well, but at other angles (e.g. vertical) focus is poor. The condition in which images oriented at different angles come to focus at different locations is known as astigmatism. Finally the condition in which the eyelens becomes inflexible and cannot change its shape in order to allow focus on close objects is known as presbyopia. Presbyopia is an almost inevitable consequence of aging, although when it begins varies from individual to individual.
The following webpage gives very nice illustrations of these common eye problems and illustrates how lenses are used to correct them.
Hyper Physics on Common Eye Defects
QUESTIONS on Optics of the Eye
Last Mofified Sunday, 19-Oct-2003 fleishml@union.edu



