Laser Fusion
To understand something about our attempts at controlled fusion as an "infinite" source of energy for the future, we first need to return to the atomic nucleus and learn a bit more. Recall that the nucleus contains almost all of the mass of an atom, but is located in a tiny fraction of the atom's volume. Containing the protons and neutrons, collectively known as nucleons, the nucleus is a composite structure that has a large amount of energy. Remember also that the nucleus is held together by the hadronic (or strong) nuclear force, a force that is the same for all nucleons and is independent of the electric charge. This force is needed to overcome the large repulsive electric force due to packing protons, all of like positive charge, extremely close together inside the nucleus, with a size of a few Fermi, a unit standing for 10-15 m.
Different species of nuclei are labeled in a standard way by the number of protons, Z, the atomic number (also reflecting the positive charge and characterizing the species of nucleus), and the total number of nucleons (protons plus neutrons), A (proportional to the total mass of the nucleus, and therefore also known as the mass number). For example, the hydrogen nucleus is labeled as 11H, where the superscript is A and the subscript is Z and the letter for the particular nucleus is determined solely by Z. The nucleus of deuterium, the deuteron, is 21H, while that of tritium is 31H. These each have one proton, so they are different forms of hydrogen, with one or two neutrons also in their nucleus. Their chemical properties are essentially identical since they each have only a single electron. Another example is the iron 56 nucleus 5626Fe. Note that the subscript number is redundant because the name of the element indicates the number of protons already, 1 for hydrogen and 26 for iron. Recall that isotopes are different forms of the atom all with the same number of protons, but different numbers of neutrons. Nuclides is the term used for their corresponding nuclei.
Nuclei behave similarly to atoms as a whole in that they also have a set of energy levels with a ground state and excited states, and with different nuclides having different characteristic energy levels. What is very different is that the values of the energy levels are so much greater because of the much larger forces holding the nucleons in the nucleus, compared to the forces on the electrons holding them in the atom. Electrons in atoms are bound with energies on the order of electron volts, while nucleons are bound in the nucleus with energies of millions of electron volts. While electron bonding leads to chemistry and chemical energies, nucleon bonding leads to nuclear reactions with energies roughly a million times greater.
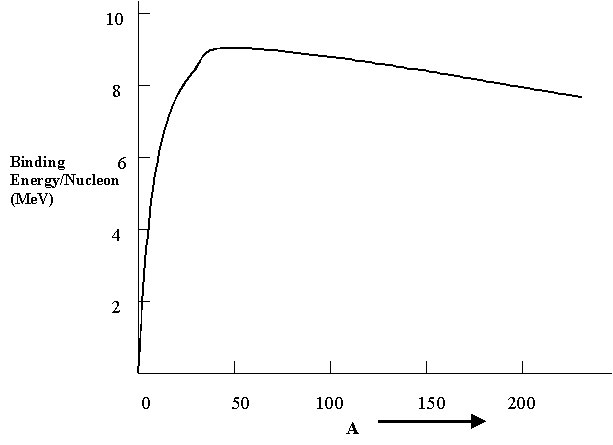
The most important graph relating to nuclear energies is the one below showing the binding energy per nucleon for the different nuclides that exist. Greater binding energy means that the nucleus is held together tighter and is therefore more stable. Note that binding energies are really negative energies, just as in atoms, and a greater binding energy means that the total energy of the nucleus is actually lower, or more negative. As you can see the general behavior of the graph is that as the mass number A increases, the binding energy increases up to a maximum at the nuclide iron-56, 56Fe, and then decreases slowly and steadily with increasing A. The nucleus of normal hydrogen has 0 binding energy because it is a single proton alone. Note that the vertical scale is in units of MeV (or millions of electron volts). This graph contains a huge amount of information and is the explanation of both the processes fission and fusion, explained below. The fundamental idea is the conversion of mass to energy, according to Einstein's equation E = mc2 . As we know, c is a very large number, and so small decreases in the net mass lead to large energies liberated.

Consider first the larger A nuclei. They have a binding energy per nucleon that is about 0.8 MeV lower than smaller nuclei with A on the order of 100. This implies that they are somewhat less stable and, under the right circumstances, will undergo nuclear fission, splitting into two smaller nuclei and often liberating several neutrons as well. The total binding energy of the two product nuclei, called daughters, is greater than that of the initial high A nucleus, and this is the driving force that causes the fission. Thus, the total potential energy of the daughters is lower than the starting potential energy, with the excess released as kinetic energy of motion. If we calculate the net release of energy for a large nucleus, say 235U, we find that it is about (0.8 MeV/nucleon) x (235 nucleons) = 188 MeV for every 235U nucleus that undergoes fission. Compare this with the couple of eV released in atomic (chemical) reactions - it is some 100,000,000 times more energy per atom.
The first application of fission was the atomic bomb, in which the fission occurred in an uncontrolled way and released huge amounts of destructive energy as well as radioactivity from the long-lived radioactive products produced. Released neutrons produced a chain reaction, in which each fission produces several others, which causes the rate of energy release to grow dramatically. Fortunately for mankind, these weapons have not been used again up to this point.
We have also learned how to harness fission in controlled ways in order to generate useful energy in nuclear power plants. Very briefly, these power plants use the kinetic energy generated in a controlled nuclear reaction to heat water, turning it to steam which is used to drive steam turbines to produce electricity. The reactions are controlled using neutron absorbing control rods to regulate the number of neutrons available to induce fission. A perfectly controlled reaction in a steady-state condition will produce one new fission for each fission, keeping the rate of energy production constant. By regulating the absorption of neutrons by the control rods, the reaction can be kept stable and energy production rates made constant. Problems that have occurred at nuclear power plants (notably Chernobyl and Three Mile Island) have been due to overheating due to poor control and excess energy release over that which could be absorbed by the cooling water.
Let's now return to the binding energy graph above and consider the smallest nuclei. These have substantially lower binding energy per nucleon than larger ones and, under the proper conditions can be made to fuse together to produce a larger A nucleus in a process called nuclear fusion. For example, if two deuterons fuse together to form a helium-4 - or 4He - nuclide in the following reaction: 2H + 2H > 4He + 23 MeV, there is an enormous amount of energy release per nucleon, amounting to about 6 MeV per nucleon. This is a common nuclear reaction that occurs in the interior of stars. The most common fusion reaction is the proton - proton cycle occurring in most stars. It is a series of three reactions:
1H + 1H > 2H + positron + neutrino;
followed by 1H + 2H > 3He + photon
ending with 3He + 3He > 4He + 2 positrons + 25 MeV energy
The net result of this reaction is the conversion of hydrogen to helium with the production of some lighter weight positrons, neutrinos and photons, together with a large amount of energy. When stars are hotter or have depleted much of their hydrogen, other reactions can occur, such as the fusion of three helium-4 nuclides to produce carbon-12. In fact all of the heavier elements in the universe were produced in nuclear reactions within stars. These heavier elements were spread to parts of the universe by stellar explosions - supernovae. Every heavy element on the earth was made from this process. In fact, we are all made of stardust!!
On earth, man-made fusion processes are limited to a single step since it is very difficult to produce in a laboratory or future power plant the extremes of temperature and pressure of the interiors of stars. Two of the possible fusion reactions that have been produced in laboratories are
deuteron-deuteron fusion: 2H + 2H > 3H + 1H + 4 MeV,
or, tritium-deuteron fusion 3H + 2H > 4He + neutron + 17.6 MeV.
In order to produce nuclear fusion three criteria must be met: high temperature (greater than about 100 million degrees), high density of nuclei (so that collisions are frequent), and the nuclei must remain together for a long enough time to fuse and release energy. Two different schemes have been used to try to confine nuclei to a tiny space and heat them in order to produce fusion. One involves magnetic confinement using a Tokomak while the other involves using high powered lasers to provide the energy in a scheme known as inertial confinement.
To give you some idea of the enormous potential of nuclear fusion in generating useful energy, 1 kg (just over 2 pounds) of sea water, which contains only about 0.015% deuterium, if completely fused to produce energy will produce more than 30 times the energy of the same amount of gasoline. More important perhaps are the facts that, first, the earth has essentially an unlimited supply of sea water, and second, the products of fusion are not dangerous, as are the products from nuclear fission. Nuclear fusion is very difficult to achieve. If the high temperature and density conditions needed are not met or sustained for sufficient time, the reaction will not proceed. In other words, there is no possibility of a "run-away" nuclear fusion reaction in a laboratory or power plant.
Inertial confinement works by starting with a fuel pellet, typically a deuterium/tritium enriched target mixture about the size of a pea, that is heated using some kind of a driver that heats the pellet using photons or ions and also compresses it. When the density of the fuel reaches about 20 times that of lead the fuel "ignites" at a temperature of 100 million degrees and undergoes nuclear fusion producing a large excess in heat energy release over the energy input from the driver. The goal is to produce 100 times the input energy in a power plant with a long life-time that runs on cheap fuel pellets. Current work in the US is at Lawrence Livermore Laboratory in the National Ignition Facility (NIF) where a sports stadium-sized facility is under construction (nearly completed) in order to bring 192 intense laser beams with a total energy of 1.8 million Joules together on a 3 mm fuel pellet that sits at the center of a 1 million pound target chamber that is 10 meters in diameter.
General web reference on fission and fusion
