![]()
Exhumation of the Cordillera Blanca, Northern Peru, based on apatite fission track analysis
Matthew James Montario
Reccomended citation:
MONTARIO, MATTHEW JAMES, 2001, Exhumation of the Cordillera Blanca, Northern Peru, based on apatite fission track analysis, Department of Geology, Unpublished Thesis, Union College, Schenectady, New York, 55 p.
ABSTRACT
The Cordillera Blanca in the Northern Peruvian Andes makes up the highest peaks of the Peruvian Andes including the 6768 m peak of Huascarán. The N-S oriented Cordillera Blanca Normal Fault (CBNF) cuts the Cordillera Blanca along the western side of the mountain range with a 35-45o dip for about 210 km.
Apatite fission-track analysis of six samples from granites in the footwall yield ages that range from 1.8 to 4.2 Ma. Specific samples give the following ages: PE-2, a granite from Cojup at ~4150 meters, is 01.8 Ma (± 0.7 Ma); PE-3, a Quartzite from Pastourri at ~4960 meters, is 04.2 Ma (± 3.5 Ma); PE-4, a Granite from Ishinca at ~4930 meters, is 02.7 Ma (± 0.5 Ma); PE-5, a Granite from Llanganuco at ~3860 meters, is 02.9 Ma (± 0.5 Ma); PE-6, a Granite from Llanganuco at ~3850 meters, is 03.0 Ma (± 0.6 Ma); and PE-7, a mylonitic Granite from Llanganuco at ~3480 meters, is 02.3 Ma (± 0.9 Ma). Assuming a closure depth for apatite of about 3.2 km, and an average cooling age of about 2.8 Ma, the overall exhumation rate would have been approximately 1.1 km/My.
Assuming a dip of 35o on the fault, and 3.2 km of exhumation, the total slip on the CBNF has been ~5500m in the last 2.8 Ma. This slip integrated over the average cooling age gives a slip rate on the CBNF of approximately 1.9 mm/yr. Displaced moraines and trench studies across the Cordillera Blanca Normal Fault indicate a vertical uplift of about one mm/yr. These and other data indicate that the Cordillera Blanca has been exhumed along its entire length an average rate of 1.0 km/My since intrusion of the Cordillera Blanca Batholith at ~8.0 Ma.
Introduction
Geologic Background:
The subduction of the Nazca plate under the South American continent has resulted in the formation of the Andean magmatic arc. The whole arc is formed by the subduction of oceanic crust under the continent, but magma genesis varies dramatically from north to south. Based on magmatic variation, the Andes can be divided into four zones: 1) the northern volcanic zone which includes Venezuela, Colombia and Ecuador, 2) the central plutonic zone in Peru, 3) the central volcanic zone which includes Bolivia and northern Chile, 4) the southern plutonic zone in central Chile (McNulty et. al., 1998). The Cordillera Blanca is located in the Northern Peruvian Andes and is part of the central plutonic zone (Figure 1).
The Cordillera Blanca is mainly composed of a large granodiorite batholithic complex that has a uranium-lead age of 8.2 ± 0.2 Ma (McNulty et. al., 1998). The batholithic rock makes up the highest peaks including the 6768 m peak of Huascarán and are exposed over 4.4 km of vertical relief. The main rock component of the batholith is granodiorite, which makes up ~80 to 90 % of the exposed intrusive rock. The remainder of the rocks are mostly tonalite and diorite (McNulty et. al., 1998). Exhumation of the batholith and adjacent metamorphic rocks has occurred along the Cordillera Blanca Normal Fault (CBNF) that extends for some 210 km along the margin of the mountain range (Schwartz, 1988). The fault scarp has a dip of ~35-45o to the west, and it is well defined north of Huaraz but is poorly defined to the south (Schwartz, 1988). The Cordillera Blanca Normal Fault has been highly active during the late Quaternary (Schwartz, 1988; Farber et. al., 2000).

View to the north down the Rio Santa river at Huascarán.
This area has about 4000 m of relief. Photo: J.I. Garver
Background on Fission Track Dating:
Fission track analysis is the study of nuclear tracks in insulating solids formed by the natural or induced fissioning of uranium. Tracks are formed when unstable atoms in an insulating solid undergo fission. The most commonly accepted theory behind fission track formation is the ion spike model (see review in Gallagher et. al., 1998) (Figure 2). The fission process creates energy, approximately 200MeV, most of which is transferred to the products of the fission process in the form of kinetic energy. The two atom fragments travel in opposite directions leaving a tubular shaped damage zone in the crystal. These tracks are produced because the fragments of the atom are charged and strip electrons from other atoms as they pass by. This stripping of electrons causes the atoms in the insulating solid to repel each other creating a cylindrical void of disorder in the solid (Wagner & Van Den Haute, 1992). In geologic settings, virtually all tracks formed in zircon and apatite are from the natural fissioning of 238U. The fission half-life of other isotopes, including 235U and 232Th, are too long to be considered in typical natural settings (Gallagher et. al., 1998). The mass of a track-forming particle needs to be 30 atomic mass units or more, or else it is not heavy enough to rip through the crystal lattice.
The latent track produced in the solid is very small, only about 10-15mm in length, and can only be seen using an electron microscope (Wagner & Van Den Haute, 1992). Fission track analysis was not widely used for this reason until the 1960s when Fleischer et al. (1964) discovered that tracks could be viewed optically if enlarged by chemical etching. This etching process opens up the latent track because the damage from the fission process weakens the surrounding structure of the solid. It soon became apparent that, after etching, fission tracks could be used as a dating method. The only difference is that physical damage is the product of the fission process instead of a daughter element. Dating a sample requires a high enough concentration of uranium and long enough time to produce a detectable number of tracks. However, if too much 238U is present, the track density is so high that counting the tracks in the sample is impossible using conventional methods. Usable concentrations can range anywhere from approximately 1-1000 ppm over geologic time scales of 1-500 Ma. Common minerals with appropriate concentrations of uranium include sphene, apatite and zircon (Gallagher et. al., 1998).
The fission track age of a sample is determined using mathematical formulas similar to those of other radioactive decay dating methods. Dating a sample requires an estimate of the abundance of the parent isotope and the presence of fission tracks. To estimate the number of tracks, the sample is etched and the exposed tracks are counted. Determination of the concentration of 238U is more complicated, and many different methods can be used, including the population method and the external detector method (Gallagher et. al., 1998). The method for determining the concentration of 238U is to induce fission in 235U by irradiating the sample with low energy ("slow") neutrons. The tracks formed by this process can be counted and therefore the concentration of 235U can be determined, and because the ratio of 235U/238U is constant in nature, the concentration of 238U can then be determined. The most commonly used approach to fission track dating is the external detector method (Figure 3). In this method, a mica detector with a very low uranium concentration is placed on top of a sample that has been polished and etched. The irradiation of the sample causes tracks to form in the mica when the fission particles from the sample make a track in the mica surface. The tracks formed on the mica are from uranium present in the sample (235U), and close enough to the etched surface to create a track in the mica. The mica is then etched and the tracks counted. The external detector method allows each individual grain or parts of each grain to have its uranium concentration determined, avoiding the assumption of uniform distribution inherent in the population method (Gallagher et. al., 1998).
Annealing:
Fission tracks are not stable and can shorten or even disappear if the sample spends considerable time at elevated temperatures. The process by which tracks fade is called annealing, and the main control on annealing is temperature. Tracks anneal when the thermal stability limit, or the temperature at which the tracks heal, is reached. Annealing occurs when the displaced atoms return to the positions they were in before track formation. It was originally believed that annealing took place at random points along the track (Fleischer et. al., 1964). However, recent studies show that annealing begins at the ends of the tracks and causes the tracks to shorten (Wagner & Van Den Haute, 1992). This shortening can affect age determinations because if a track shortens it has less chance to cross the etched surface. In this case, a smaller number of tracks would be counted and a younger age would be obtained (Wagner & Van Den Haute, 1992). Different minerals have different thermal limits and can be more or less resistant to annealing. Several factors may affect annealing, such as temperature, chemical composition, and time, but temperature is the most important (Gallagher et. al., 1998).
The temperature at which annealing completely erases tracks in apatite is ~80-110oC depending on the cooling rate and chemical composition (Wagner & Van Den Haute, 1992). The accepted closure temperature for apatite is about 100oC, but partial annealing occurs at temperatures as low as 60oC given sufficient time. This lower end of the annealing temperatures is called the partial annealing zone or PAZ. Due to low closure temperatures apatite is a particularly sensitive recorder of cooling history. Most other minerals, such as sphene and zircon, have closure temperatures at or above 200oC. If both apatite and some other mineral such as zircon are present in a rock, the differences in age can reveal the cooling history of a rock (Green et. al., 1996). This cooling history is revealed because the high closure temperature is reached for the first mineral. Then later during exhumation the lower closure temperature of the apatite is reached. The difference between these ages is the cooling time for that rock over that temperature interval. The reset age can be of importance in studying the thermal history of an area, because this age indicates the time an area underwent severe exhumation. Apatite can also be effective in determining ages of thermal events in the upper part of the earths crust. A problem with rocks from lower in the crust is that the apatite could be exposed to a temperature that resets its radiometric "clock" but this temperature is not high enough to reset the other mineral present. This is more of a problem for determining the rates of uplift in an area. If the tracks are reset the age is going to be much younger and the rates of uplift incorrect.
The composition of apatite may be an important factor in determining annealing rates (Gallagher et. al., 1998). Chlorapatite has been shown to be more resistant to annealing than other forms (Gallagher et. al., 1998). There is still debate as to what affect other compositions have on track annealing. Fission tracks parallel to the c-axis in apatite are more resistant to annealing than tracks in any other orientation. Therefore, while counting tracks in apatite an inaccurate age may be obtained if the tracks are not parallel to the c-axis. Another complication that can affect annealing is crystalline imperfection of the mineral. If imperfections or inclusions are prevalent in a grain then it is usually not counted because there are many other grains in the sample that can be counted (Wagner & Van Den Haute, 1992).
Apatite and Exhumation:
Uplift is the process by which the land surface and rock column are raised above sea level. Exhumation is the process by which rocks are brought to the surface by erosion and faulting. Apatites in exhumed rock start at a certain depth below the earths surface where tracks are completely annealed (Gallagher et. al. 1998). As exhumation begins, the rock moves upward in the rock column with respect to the surface (Figure 4). This upward movement causes the temperature of the apatite to decrease and eventually reach the point where tracks are preserved. The closure temperature for apatite is about 100oC to 110oC and at this point the fission track clock in the apatite starts. The depth at which this occurs can be determined only if the geothermal gradient in a particular area is known. If both the age and depth are known, then the rate of exhumation can be calculated by dividing the depth below the surface at which 100-110oC is reached by the calculated age of the apatite. This calculation gives an approximate exhumation rate in meters per million years.
Use of Fission Track Analysis:
Fission track ages can be used in many different studies of geologic processes. These include determining sedimentary provenance studies, dating of orogenic or mountain building events, and histories of sedimentary basins. Of these, apatite fission track dating is used mostly in orogenic and sedimentary basin histories. Provenance studies use detrital grains with tracks that formed in the source rock. These studies are based on the burial and transport of sediment. Due to the low closure temperatures of apatite it has a limited use in this type of study because the rocks may be buried and tracks reset. Zircons are much better for these studies because they are more resistant to physical weathering, and can tolerate wider temperature fluctuations common in buried basins (Garver et. al. 1999).
Apatite fission track dating has also been applied extensively to understanding the evolution of orogenic belts (Gallagher et. al. 1998). If the dates of many different radiometric-dating schemes, such as U/Pb or Ar/Ar are used, a thermal decay curve can be constructed. Because different dating schemes have different closure temperatures, they yield different ages that track orogenic development. Most other dating schemes have high closure temperatures of 250oC or more. Fission track dating allows the sample to be dated for lower closure temperatures. It is also important to prove that no significant annealing has occurred after closure because this annealing can result in an age determination unrelated to orogenesis. In this case, the calculated age would be an apparent age, perhaps unrelated to orogenesis. The length distributions of spontaneous and induced tracks can help determine if tracks in the original samples are partially annealed.
Methods
Rocks were collected from fresh, accessible outcrops in the field. About 2-4 Kg of crushed sample was pulverized and then the apatite and zircon were separated using standard separation techniques at the Institute of the Lithosphere (Moscow, Russia). This technique involved heavy liquids and magnetic separation.
Apatite grains were mounted in epoxy on a glass slide, ground, and polished using 9mm and 1mm diamond paste. Samples were then etched in 5m HNO3 for 20 seconds at 20-22oC. Etched samples were covered with pre-annealed, fresh-cleaved mica. Samples were irradiated with a nominal fluence of 8x1015 n/cm2 at the Oregon State nuclear reactor. After irradiation, mica was etched in 48% HF for 15 minutes. Samples and irradiated mica were mounted on glass petrographic slides.
Glass monitors (CN-1), placed at the top and bottom of the irradiation package were used to determine the fluence gradient. All samples were counted at 1250x using a dry 100x objective (10x oculars and 1.25x tube factor) on an Olympus BMAX 60 microscope fitted with an automated stage and a Calcomp digitizing tablet. Apatite fission track ages (± 1s) were determined using the Zeta method. Ages were calculated using the computer program and equations in Brandon (1992). A Zeta factor of 106.16 ± 4.45 (± 1 se) is based on eight determinations from both the Fish Canyon Tuff (3) and the Durango apatite (5). All ages with c2 > 1% are reported as pooled ages, otherwise, Central ages are used.
Data
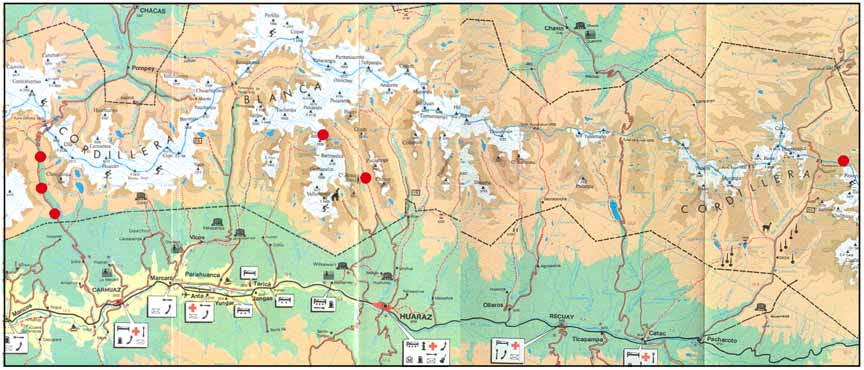
All the samples counted have young ages, ranging from 1.8 Ma to 4.2 Ma. Sample PE-2 is a granite from Cojup at an elevation of ~4150 meters. This sample had very few minerals other than apatite on the mount and was easy to count, moderate uranium concentration. Sample PE-3 is a quartzite from Pastourri at an elevation of ~4960 meters. This sample was very difficult to find a good apatite grains and only five grains were counted, and thus the error is high. Sample PE-4 is a granite from Ishinca at an elevation of ~4930 meters. This sample had minerals other than apatite on the mount and but was still a good sample for counting, and the apatite have high uranium concentrations. Sample PE-5 is a granite from Llanganuco at an elevation of ~3860 meters. Sample 5 had many good grains for counting, and grains have high uranium concentrations. Abundant inclusions of zircon in the apatite caused difficulty with counting the mica; these grains were avoided where possible. Sample PE-6 is a granite from Llanganuco at an elevation of ~3850 meters. Similar to sample five, had many good grains for counting with good uranium concentrations, but some zircon inclusions. Sample PE-7 is mylonitic granite from Llanganuco at an elevation of ~3480 meters taken from very near the CBNF. Sample 7 is very similar to sample five and six, inclusions of zircon in grains and a medium to low uranium concentration. The summary of all age calculations for the samples is in Table 1. A plot of the sample ages versus the elevation of the samples does not show any correlation between the two (Figure 5). Sample locations are also included in Table 2. All data are in Appendix A and Appendix B.
Table 1: Apatite fission track data Cordillera Blanca, Peru
|
South |
Elev |
RhoS |
Ns |
RhoI |
Ni |
RhoD |
Nd |
n |
Chi2 |
Age |
err |
err |
U (ppm) |
|
South |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PE-3 |
4960 |
6.98 x 103 |
01 |
3.35 x 105 |
0048 |
3.331 x 106 |
2179 |
05 |
100 |
04.2 |
-3.5 |
+7.5 |
04.0±1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Central |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PE-2 |
4150 |
9.28 x 103 |
06 |
9.10 x 105 |
0588 |
3.313 x 106 |
2167 |
15 |
100 |
01.8 |
-0.7 |
+0.9 |
10.9±1.0 |
|
PE-4 |
4930 |
3.78 x 104 |
22 |
2.52 x 106 |
1466 |
3.350 x 106 |
2191 |
15 |
19.9 |
02.7 |
-0.5 |
+0.6 |
30.0±1.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
North |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PE-5 |
3860 |
4.69 x 104 |
31 |
2.86 x 106 |
1894 |
3.369 x 106 |
2203 |
15 |
22.0 |
02.9 |
-0.5 |
+0.6 |
33.8±1.9 |
|
PE-6 |
3850 |
3.61 x 104 |
22 |
2.20 x 106 |
1340 |
3.387 x 106 |
2214 |
15 |
37.6 |
03.0 |
-0.6 |
+0.7 |
25.9±1.7 |
|
PE-7 |
3480 |
9.44 x 103 |
06 |
7.54 x 105 |
0479 |
3.406 x 106 |
2226 |
15 |
100 |
02.3 |
-0.9 |
+1.2 |
08.8±0.9 |
Note: In this table, Rhos is the density (cm-2) of spontaneous tracks and Ns is the number of spontaneous tracks counted; Rhoi is the density (cm-2) of induced tracks; and Rhod is the density (cm-2) of tracks on the fleunce monitor (CN1); n is the number of grains counted; and Chi2 is the Chi-squared probability (%). Apatite fission track ages (± 1 SE) were determined using the Zeta method, and ages were calculated using the computer program and equations in Brandon (1992). A Zeta factor of 106.16 ± 4.45 (± 1 se) is based on eight determinations from both the Fish Canyon Tuff (3) and the Durango apatite (5). All ages with Chi2 > 1% are reported as pooled ages, otherwise, Central ages are shown. Glass monitors (CN-1), placed at the top and bottom of the irradiation package were used to determine the fleunce gradient. All samples were counted at 1250x using a dry 100x objective (10x oculars and 1.25x tube factor) on an Olympus BMAX 60 microscope fitted with an automated stage and a Calcomp digitizing tablet. Elevations are given in meters.
Interpretation
There are two features associated with the exhumation that need to be taken into account for analysis of the uplift and exhumation Cordillera Blanca. One is the total exhumation rate and the other is the horizontal slip rate of the Cordillera Blanca Normal Fault, which is driving exhumation. The closure temperature for apatite is between 80 and 100oC. With closure temperature and the fission track ages, the exhumation rate in the Cordillera Blanca can be estimated. In this system, DT is equal to the temperature of the sample at the surface minus the closure temperature. The temperature of the sample at the surface was ~10oC, if the closure temperature was 100oC for the apatite then DT=10oC -100oC which is 90oC. Using the geothermal gradient of the Cordillera Blanca, which is estimated to be 25oC to 30oC, the closure depth is 3.2 km (see Garver et. al., 1999) (Figure 6). For a closure depth of 3.2 km the exhumation rate is about 1 km/My. Because the average age of the samples is about 2.82 million years, the overall exhumation rate is approximately 1.14 km/My.

View of the Cordillera Blanca Normal Fault from the hills outside Huaraz.
View to the north. Photo by J.I. Garver
The Cordillera Blanca is inferred to have been intruded at a pressure of 3 kb (McNulty & Farber, 1999). The Batholith has a U/Pb age of 8.2 ±0.2 (McNulty et. al., 1998) and the total uplift for the batholith is 9000 meters, in this case the long-term (last ~8 Ma) exhumation rate is about 1.07-1.12 km/My.
These data may also be used to estimate slip on the Cordillera Blanca Normal Fault (CBNF) assuming the fault is responsible for most of the exhumation. The horizontal slip rate can be estimated by restoring rock downward in the fault (Figure 7). To do this, several factors must be taken into account for the calculation to be correct. For the Cordillera Blanca, the closure depth is about 3.2 km. Using the dip of the fault, which is 35o, and the 3.2 km of exhumation, the total slip of the fault is 5500 meters since c. 3 Ma. This gives a slip rate on the CBNF of approximately 1.98 mm/yr.
Displaced moraines and trench studies across the Cordillera Blanca Normal Fault indicate a vertical uplift of about 1.0 mm/yr. Schwartz (1988) studied moraines near Quebrada Queroccocha and trenches in two other areas. The moraines are dated at 11,000 to 14,000 years and are displaced 12-15 meters. In addition, younger lacustrine sediments were displaced 7.5-8.0 meters. The slip rates for the Quebrada Queroccocha are thus 0.86-1.36 mm/yr. Schwartz (1998) states that scarp profiles indicate five to seven tectonic events in this area with a recurrence interval of about 1000 to 3000 years. In an earlier study, Schwartz and co-workers estimate the extensional strain rates to be approximately 2.0 mm/yr across the Cordillera Blanca (Schwartz et. al. 1984). If this estimate is correct, and if our calculations above are correct, the CBNF must account for ~80% of the extensional strain.
Farber and others (2000) did a similar study of offset features along the CBNF using cosmogenic dating. Several moraines were dated using in situ produced 10Be and 26Al (Farber et. al. 2000). Moraines and fluvioglacial material were located around Quebradas Cujup and Llaca, Q. Tuco, Q. Querrococha and Quebrada Huaytapllana. For the Q. Querrococha terraces dated 19 Ka, the vertical offset was about 15 meters. This offset yields an uplift rate of ~0.8 mm/yr. For Q. Tuco the rate is ~1.2 mm/yr, and for Quebradas Cujup and Llaca the rate is about 1.3-1.8 mm/yr. Quebrada Huaytapllana was still being dated at the time of writing. These data together suggest that vertical exhumation in the Cordillera Blanca has been at least one mm/yr for the past 20 Ka. Higher values of up to 3.0 mm/yr suggested by Farber et al. may indicate more rapid exhumation in the center portion of the Cordillera Blanca.
A recent study by Rodbell and Seltzer (2000) dealt with deglaciation chronology along the Rio Negra in the central segment of the CBNF. Several of the moraines in this area were dated and offsets measured. These moraines indicate a vertical uplift of ~1.0 mm/yr for the central segment.
Conclusions
Cosmogenic and deglaciation chronology uplift rates agree with the apatite fission track ages and exhumation rates determined in this study. The Cordillera Blanca has been exhumed along its entire length an average rate of 1.0 km/My for the last 8.0 Ma. The central portion of the Cordillera Blanca could be exhumed at a slightly faster rate than either end, but more work would be required to confirm this. The fact that the apatite sample closest to the end of the batholith is the oldest would support this hypothesis and it would probably be worthwhile to date rocks at the other end of the Cordillera Blanca. The Cordillera Blanca Normal Fault has a long-term average slip rate of ~2.0 mm/yr as determined from the apatite ages. The fault does not actually move at this rate, because offsets in moraines suggest that it slips episodically (Schwartz, 1984; Schwartz, 1988; Farber et. al., 2000). The data collected in this study are closely related to other studies done on glacial moraines and fluvial terrace deposits and seem to support the current exhumation rates in the Cordillera Blanca.
ACKNOWLEDGEMENTS
I would especially like to thank Professor John Garver for being my thesis advisor. Professor Garver has been a guiding force in my career, between classes and work he has taught me a great deal.
I would also like to thank the Geology Department for all the experiences that have been offered to me. I dont believe that any other department at this College has such great professors who do work in so many interesting fields. The amount of fieldwork that I have been able to do during my undergraduate career has been incredible. I hope that in my future I have the same opportunities.
References
Farber, D., Hancock, G., Finkel, R., Gallagher, S., Palacios, O. The
Kinematics of Continental Detachment Faulting: Slip rates along the Cordillera
Blanca Detachment fault deduced from in situ produced Cosmogenic Radionuclides 10Be
and 26Al. Eos,
Transactions, American Geophysical Union, 2000 Vol. 81, No. 48, P. F35
Fleischer,
R.L., Price, P.B., Walker, R.M. The Ion Explosion Spike Mechanism for Formation
of Charged Particle Tracks in Solids. Journal of Applyed Physics, 1965a, Vol.
36, P. 3645-3652
Gallagher,
K., Brown, R., Johnson, C., 1998, Fission Track Analysis and Its Applications to Geological Problems. Annual Rev.
Earth Planet Science, Vol. 26, P. 519-572
Garver,
J.I., Brandon, M.T., Roden-Tice, M., Kamp, P.J.J., 2000, Exhumationhistory of
orogenic highlands determined by detrital Fission track
thermochonology.Geological Society Special Paper, London.
Green,
P.F., Duddy, I.R., Gleadow, A.J.W., Tingate, P.R., Laslett, G.M., 1986, Thermal
Annealing of Fission Tracks In Apatite.
1. A Quantitative Description. Chemical Geology (Isotope Geoscience Section),
Vol. 59, P. 237-253
McNulty,
B.A., Farber, D.L., 1998, The Cordillera Blanca fault zone; a deep seated
detachment in the Peruvian Andes. Geological Society of America, Vol. 30, No.
7, P. 238
McNulty,
B.A., Farber, D.L., Wallace, G.S., Lopez, R., Palacios, O., 1998, Role of plate
kinematics and plate-slip-vector partitioning in continental magmatic arcs:
Evidence from the Cordillera Blanca, Peru. Geology: September, Vol. 26, No. 9,
P. 827-830
Rodbell,
D.T., Seltzer, G.O., 2000, Rapid
Ice Margin Fluctuations during the Younger Dryas in the Tropical Andes.
Quaternary research, Vol. 54, No. 3, P. 328-337
Schwatz,
D.P., Salazar, H., Felix, O., Santucci, C.A., Arnt, A., La Cruz, J., Farfan,
M., 1984, Late Quaternary normal faulting, recurrence intervals, and slip rates
along the Cordillera Blanca fault zone, northern Peruvian Andes. American
Geophysical union, Vol. 65, No. 45, P. 1082
Schwartz,
D.P., 1988, Paleoseismicity and Neotectonics of the Cordillera Blanca Fault
Zone, Northern Peruvian Andes. Journal of Geophysical Research, Vol. 93, No.
B5, P. 4712-4730
Summerfield,
M.A., 1991, Global Geomorphology: An introduction to the study of landforms.
Longman Scientific & Technical, New York. P. 373-400
Wagner,
G., Van Den Haute, P., 1992, Fission track Dating. Solid Earth Sciences
Library, Kluwer Academic Press, Boston, Vol. 6, P. 47-118
Back to Union Fission Track Home
page
Back to Home page for J.I.
Garver
Back to Union
Geology Department
This document can be located from
http://idol.union.edu/~garverj/FT/FThome.html
All rights reserved. No part of the document can be
copied and/or redistributed,
electronically or otherwise, without written permission from: J.I.Garver, Geology Department, Union
College, Schenectady NY, 12308-2311, USA.
Last Revised: 3 January 2000