Introduction
What happens when light falls onto an object? The answer to this question depends a great deal on the model that we want to use to describe the interaction of light with matter. At the macroscopic level, we may say that light is reflected or absorbed. For example, when sun light falls on our hand part of it gets scattered, as diffuse reflection. (This allows us to see our hand, because this reflected light reaches our eye and forms the image of our hand in our retina.) While some of the sun light is absorbed by our hand. We also sense this portion of the light; it heats our skin. What aspect of the light causes it to be reflected and which aspect of it makes it heat up our skin?
As we discussed earlier, light is electromagnetic wave. The wavelength (or its frequency), and its amplitude are the two primary physical factors that describe its properties. The more intense the light, the higher is the amplitude of the electromagnetic wave. In the particle (photon) picture, this amounts to the number of photons that are "in the light" per unit of time. As in the case of bullets fired by an automatic machine gun, the more bullets fired per second, the "stronger" the amplitude. Continuing with this analogy we notice that the full strength of the gun depends both on the number of bullets it fires as well as on the "strength" of each bullet. It is the wavelength (or frequency) of the light that determines the "strength" of a single bullet. To be more precise, the energy of a single photon, as we discussed earlier, is directly proportional to its frequency (and thus inversely proportional to its wavelength). So, the overall strength of the light is a function of both the number of photons it is delivering per second and the frequency of each photon.
The above discussed dependence of light energy on photon energy as well as on photon rate was not an obvious fact. In fact, it was described by Planck and Einstein at the turn of the twentieth century and won Einstein his Nobel Prize. The discovery of this interdependence of the photon rate and per photon energy not only affected the way we think of light's total energy, but it also has modified our understanding of how light interacts with matter. To examine this interaction further, it is useful to think of matter as composed of atoms and to ask the question how does light (photons) interact with an atom?
Atom-Photon Interaction
To begin this discussion we need to first clarify what is an atom. As a result of many experiments we now know that stable matter, whether in gas or in liquid or in solid phase, is made of collections of so called atoms. Each atom in turn is made up of a very massive nucleus surrounded with less massive, but equally charged electrons. Measurements have verified that protons and neutrons make up the nucleus of the atom. These are of nearly the same mass and size particles. Their primary difference is that protons carry a positive electric charge, whereas the neutrons are, as suggested by their name, electrically neutron. Electrons are negatively charged and are 1/2,000 times less massive than their counter part protons/neutrons. As a result, almost all of the mass of the atom is due to its number of protons and neutrons. The role of the electron is to cancel out the positive electric charge in the nucleus. Since positive and negative charges attract, the electrons bind to the nucleus and in this combination create a neutral atom.
If the protons are positively charged and therefore repel each other by their electric interaction, then how do they come together to form the nucleus; and how do they hold on to neutrons, and the neutrons to each other? The answer turns out to be in the secret of the nucleus: another much stronger force, called the hadronic force, is involved. Protons and neutrons, called nucleons, strongly attact as a result of this hadronic force when they are very close to each other. This force of attraction is much much larger than the electric force, but it falls off very quickly when the nucleons begin to separate; i.e. it has a short range of interaction. As soon as the separation distance between two protons increases, this hadronic force becomes smaller than the electric repulsion and the two protons separate from each other. Of course, two neutrons, or a proton and a neutron, have no repulsive forces. So, they continue to attract each other, but only very weakly once they begin to separate; again because the hadronic force has a "short range". In passing, it is worthwhile to mention that it is the "harnessing" of the hadronic force that provides for the nuclear energy. So, when people are talking about "atomic energy" they are really preferring to the energy within the nucleus of the atom and not the energy that holds the electrons of the atom bound to its nucleus.
When light falls onto an atom the oscillations of the electromagnetic wave causes the electron to oscillate. In this fashion the atom absorbs the energy of the light. If this atom now interacts with other atoms it can pass along the photon energy (wave oscillations). This can happen in several different scenarios. One of these is that the energy is passed on without any loss. This is clearly an ideal 100% reflection or a 100% ideal transmission. In another scenario some of the light's energy could be "used" before it is transmitted to the next atom. This scenario clearly represent absorption followed by reflection/transmission. But what happens to light when it falls onto an isolated atom? The answer to this question, turns out, to be totally anti-intuitive and somewhat beyond the realm of our understanding of macroscopic world. It is answered by quantum physics. It turns out that very small atoms form a bound structure that can absorb energy and still remain a cohesive unit provided that the energy amount is just right. If the energy amount is not of the "correct" value the atom does not absorb it at all. In the context of quantum physics these "correct" energy values create a set of energy quanta (chunks). So, it is said that the atom's energy are quantized. This is, of course, in contrast to a macroscopic case, say a child on a swing, that could absorb any value energy - any light or any strong push. So, if the photon's frequency (wavelength) is not just right, the atom totally ignores photon's presence.
Historically, it was the absorption/emission of light by individual atoms in a vapor that gave the first clues to the quantum nature of atoms. Because the atoms in a vapor tend to be very far away from one another, for all practical purposes they can be considered as isolated atoms. It was observed that when light that included photons of many energies (frequency/wavelength) was shined on an atomic vapor only very specific wavelengths of the light were absorbed. Equally, when the atomic vapor was energised (say by a high voltage source or by collisions with other atoms) it just emitted discrete wavelengths of light. Below picture shows light emitted from a tube containing hydrogen atoms in a vapor. A diffraction grating is used to separate the light of different wavelength. Notice that there are only three distict colors (wavelength/frequencies) that are visible. There is not a contnium of colors, as we see being emitted from the sun, for example.

This behaviour is similar to the case of a person climbing a ladder, as opposed to a person going up an inclined slope. The one who goes up a ladder changes its energy in steps (chunks), while the one who is going up the slope changes energy continuously. By jumping down two rung of the ladder, the ladder climber reduces two chunks of its energy. And so on. It turns out that atoms are "ladder climbers". They change their energies by going from one rung of their energy ladder (a so called energy level) to another rung (another energy level). To go up their energy ladder they absorb energy equal to the difference between the two energy levels. When they jump down from a higher level to a lower one they emit energy equal to the difference between the two levels. This energy exchange could happen by interacting with another atom, or in isolation by emitting or absorbing a photon. Pictorially, this atom light interaction is depicted as shown in the last of the three diagrams,below. The first one shows our model of energy levels. The second one depicts energy changes in the atom. The third shows energy changes through absorption or emission of photons. These energy changes that require light are called "radiative transitions".

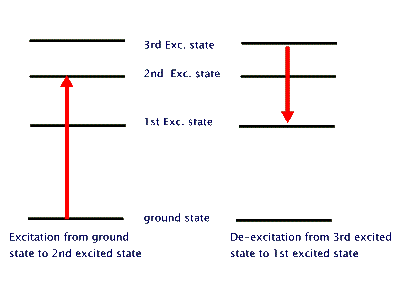
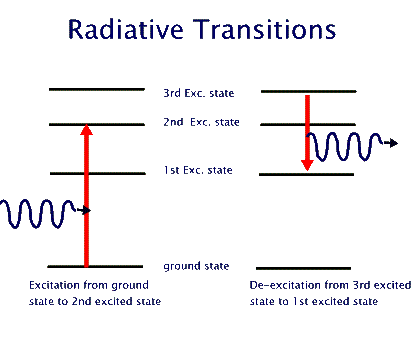
It should be noted that the atomic energy levels are not unmeasurablty sharp. They each have a characteristic "thickness" that results in creation of photons of slightly different enery even from the same set of two energy levels. This results in a small variation of photon energies, but this difference is quite measuable when we use sensitive optical devices.
From atoms to molecules to solids
What happens when two or more atoms interact and form a bound structure? Such a structure is called a molecule. How do molecules behave in the quantum world? They also have quantized energy levels, but these levels are broader. They are not a well defined value of energy, because two bound atoms not only form a sort of more complex combinations of protons, neutrons, and electrons, but they also are two interacting bound systems that could oscillate and rotate with respect to each other. All of these extra complexities creates broader energy levels, which in turn result in production of photons with a range of wavelengths/energies, even for the same transition. By the same token, these molecules can absorb photons from a range of wavelengths/energies. In this sense, then, molecules are far less choosy than the atoms.
Energy levels become even broader in the case of solids. The presence of many atoms in fixed locations relative to one another creates a so called energy bands. As a result solids are capable of emitting/absorbing photons from a very wide range of wavelengths. But there is another aspect of solids that make them behave differently from isolated atoms or molecules. If the atomic constituents of the solid happens to have one or more of its electrons loosely bound to its nucleus, then these electrons will behave as if they belong to the commune, and not an individual atom. These electrons, called the free electrons, can move from parent atom to any other neighboring atom without creating a charge deficiency, because the other commune electrons can fill-in their vacancies. A solid with this peculiar property is called a conductor. Conductors, such as metals, are made up of atomic species that have free electrons that can move from atomic site to atomic site without any difficulties. In the absence of an electric field, of course, this motion is purely random. So, there is no net flow of electricity in the solid. But when an electric field is present, then the electrons flow in the direction along this fields and in this way create an electric charge flow, referred to as the electric current.
Still another interesting feature of solids is exhibited in the case of solids that form a regular array of atoms, i.e. crystals. In these solids the individual atoms sit at regular positions, say at the corners of a cube that forms a three-dimensional network. Because of this regularity and the underlying symmetry the bulk properties of solids can be very interesting. For example, when the atoms in some crystals experience the oscillations induced by an electromagnetic wave they begin to oscillate and as a result emit "their own" electromagnetic wave in such a way that the net wave becomes transmitted at a different angle, as compared to the original direction of its flow. This, you may recognize to be nothing other than what we earlier called refraction! In another version, the back emitted waves work in unisons to add up to a unidirectional wave, that we called the reflected ray.
Both the atomic species that makes up the solid as well as its structure determine how it behaves in the presence of light. (Another determining factor is the environment that the solid is subject to, such as heat, light, etc.) For example, carbon atoms that make up the structure of your pencil's lead (there is really no lead in today's pencils) seem to absorb light in the visible range, even though they are relatively good conductors of electricity. This is because these atoms do not form a good crystal. However, the same atoms of carbon can create a crystal with remarkable properties; the diamond. Diamond is one of the strongest of materials. It is also one of the best known conductors of both electricity and of heat. More importantly, perhaps, for the humanists, it glitter because it has a very high index of refraction and as a result strongly disperses different wavelengths of light and at the same time produces many internal reflections due to its small critical angle, also a consequence of its large index of refraction. But even more remarkable from diamond are the recently discovered carbon nanotubes (a one-atom layer forming a cylindrical structure) that conduct electricity with zero resistance in the direction along their , act as an insulator in the direction along their width, and behave as a semiconductor in the direction halfway in between! These structure behave as hard as the diamond along their lengths and as soft as your pencil "lead" along their widths.
Light detection
How can light be detected? In most applications it is easier to detect flow of electric charge than to detect frow of electric field. So, the easiest way to detect light is to use it to create electric current and then detect the current flow as a measure of presence of light. This is practically the universal method that both man-made and nature made light detectors operate. The exception to this is when we convert one form of light into another before detecting the final form by the standard trick of looking for electric charge. For example the way our eye detects photons is through a chemical process in which a photon is absorbed by a molecule (rhodopsin) and a few processes down the line an electric charge is created. The flow of charge down the optical nerve creates the "detection". But as it turns out, the rhodopsin molecule does not interact well with ultraviolet (UV) light. So, typically we cannot "see" UV radiation. By placing a fluorescent material in the path of the UV we could have the material absorb the UV and re-emit at a longer wavelength in the visible. We can then see the visible fluorescence and thus "detect" the UV. But even in this case the ultimate detection is through the conversion of light (electromagnetic wave) into electric charge.
The above statement holds true when we are concerned with energy detection. But of course light has other properties that we could measure and thus infer its presence. One of these is that it has momentum and it can therefore "push" on things. This property of light is the one that is responsible for the creation of the beautiful trails of comets. Another of properties of light is its angular momentum (which earlier, in the wave description, we called polarization). This can cause rotations. So, by observing a rotation caused by light we can infer its presence. Because light emitted by most sources is random in its polarization, and because the momentum of light is not very large in comparison to its energy, we seldom concern ourselves with detecting light due to any of its properties other than its energy.
Light Production
In the most basic form light is produced by allowing an excited atom (one with more energy than its ground state) decay through a radiative transition, as discussed above. In this kind of light production we would generate photons of discrete wavelengths (i.e. energy, or frequency). The next process we could consider is by a similar transition, but now in a molecule. This would also result in creation of photons with discrete energies, but now broader. Finally, we could extend this process to the case of solids and generate continuum of wavelengths. These are depicted in the following graph:
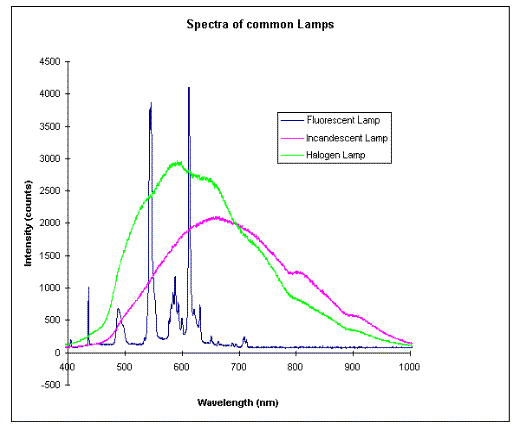
Notice that the fluorescent lamp emits atomic transition spectra that are very discrete, but these are absorbed and re-emitted by the fluorescent molecules as broader transitions and more in the visible sector of light. Both the halogen and the incandescent lamps produce a continuum of Wavelengths.
There is another method for generating light. That is by causing an oscillation of a charged object. This would result in the creation of an electromagnetic wave, that is light. But because the region of electromagnetic wave of interest to us, the visible, has very large frequency, 1014 Hz, this type of light creation is of no major interest to us.
Questions on Light Interaction with Matter
Last Modified: Wednesday, 22-Oct-2003 malekis@union.edu





