
Quantum Measurement
Measurement
Statistics & Uncertainty Estimations
Heisenberg's Uncertainty Principle
- Fourier
Transform
- Aperture & Frequency
- Heisenberg Uncertainty Principle
- Questions
Relativity Theory & Causality
Spin, Polarization, and Mixed States
Bell's Inequality
Questions & Exercises on Heisenberg's Uncertainty Principle
-
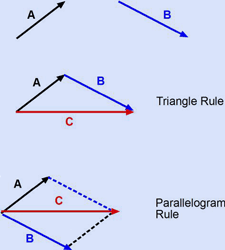 In
two-dimensional geometry we define a vector to be an entity that has
both magnitude and direction. A typical vector, then, is drawn as a
line segment with an arrowhead. These entities have their own rules
of mathematics. For example, a vector can be added to another vector
to generate a third vector, but according to the rules of "vector
addition". This rule states that to add two vectors, say A
and B, you have to place them head-to-tail by moving one
vector parallel to itself (this operation does not change the
vector). The new vector, C, which starts from the tail of one
and ends at the head of the second one is the geometrical sum of the
two vectors, i.e. C = A + B. This is
illustrated to the right and is called the triangle rule of vector
addition. Using simple geometry, show that the parallelogram
rule, which is illustrated as part ii, is equivalent to the triangle
rule of vector addition.
In
two-dimensional geometry we define a vector to be an entity that has
both magnitude and direction. A typical vector, then, is drawn as a
line segment with an arrowhead. These entities have their own rules
of mathematics. For example, a vector can be added to another vector
to generate a third vector, but according to the rules of "vector
addition". This rule states that to add two vectors, say A
and B, you have to place them head-to-tail by moving one
vector parallel to itself (this operation does not change the
vector). The new vector, C, which starts from the tail of one
and ends at the head of the second one is the geometrical sum of the
two vectors, i.e. C = A + B. This is
illustrated to the right and is called the triangle rule of vector
addition. Using simple geometry, show that the parallelogram
rule, which is illustrated as part ii, is equivalent to the triangle
rule of vector addition.
- A vector multiplied by a number (scalar) remains a vector of the
same direction, but of a different length. We define a unit vector,
i, to be a vector of length one along the +x-direction; and a unit
vector, j, to be a vector of length one along the +y-direction.
(There are our basis vectors). Use these rules to draw the vector:
- r = 3i + 5j
- s = i - 3j
- t = 2i + 3j
- What is the vector k = r + s ?
-
 Use the mathematical relationship discussed in above two
questions to prove that any arbitrary vector, say Q, could be
written as a linear combination of the basis vectors, i and
j.
Use the mathematical relationship discussed in above two
questions to prove that any arbitrary vector, say Q, could be
written as a linear combination of the basis vectors, i and
j.
- Use a spreadsheet such as Excel to create the graph of a square
wave by adding the first four Fourier components in its Fourier
Series representation (see the mathematical relationship in the
section: Fourier Series).
- Calculate the frequency of oscillations of light coming out of
the He-Ne laser that you used in question #5 of the last module (it
is 632.8 nm!).
- What is the wavelength of the radio waves that your FM receiver
captures and turns into music?
- The typical microwave oven transmits electromagnetic waves with
a wavelength of few centimeters. What is the frequency of these
waves?
- Estimate the mass and the maximum speed of a baseball. (a) What
is the maximum momentum of the baseball? (b) What is the deBroglie
wavelength of the baseball? (c) Why is this value physically
irrelevant? (The size of a proton/neutron is about 10-15 m.)
-
 The mass of a hydrogen atom is about 1.67x10-27 kg. At room
temperature it travels with a speed of about 2,700 m/s. Calculate
its deBroglie wavelength. Is this value physically relevant? (Size
of a typical atom is about 0.1 nm; that of simple molecules is about
1 nm.)
The mass of a hydrogen atom is about 1.67x10-27 kg. At room
temperature it travels with a speed of about 2,700 m/s. Calculate
its deBroglie wavelength. Is this value physically relevant? (Size
of a typical atom is about 0.1 nm; that of simple molecules is about
1 nm.)
- Does the Heisenburgh Uncertainty Principle state that we cannot
determine the position of an object with unlimited accuracy? How
about the momentum of the object? If not, then in what way does it
set a limit on our knowledge?
- Is Heisenburgh Uncertainty Principle a consequence of one measurement affecting the other; i.e. measuring the position accurately causes the velocity measurement to become inaccuate?
