Forces and Units

Equivalence of Force and Potential Energy

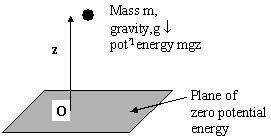It’s the largest force on a body that predominates, but it may not be easy to quantitate forces at or near the atomic level. It is often better to think in terms of the local “potentials” rather than forces. They are simply related as shown below.

Consider a body of mass m situated in a gravitational potential Φ at some distance above a plane of zero potential. The force on m is defined by

Applying to the problem at hand, the gravitational force is given by

in which is the unit vector in the (positive) direction (i.e., ) is pointing in the negative direction) and thus

              or

and, integrating:

so that Φ is simply the potential energy that the body of mass m has over the plane located at z = 0. The potential energy is different with respect to any other plane not at z = 0. Thus the defining relationship between potential and applied force is:

             or, in 1-D,

If you know the potential energy as a function of distance, you also know the force.

Quite often you have some measure of the energy but not its exact spatial dependence. For example, in the breaking of a chemical bond, the bond strength is directly related to the work to completely dissociate one part of the molecule from another. But at what separation is this complete? Theoretically, most forces acting at a distance fall off asymptotically so that it is a measure of judgment when the parts of the molecule are completely dissociated. Is it necessary to move the parts infinitely apart? In consequence of this uncertainty, statements of bond energies do not usually carry detailed information from which the force laws may be derived. Bear this in mind in when numbers are quoted for such quantities.

Following this discussion, Newton’s Law of Gravity is expressed as:

where r is the separation of the two (point) masses; thus the gravitational potential Φ is given

by integrating this expression,

where “R” is the separation between Me and m (each treated as a point mass). In SI units, Φ would be expressed in joules.