Nanotechnology

Scaling of Classical Mechanical Systems

As things change from the macroscopic to the microscopic, the ratio of forces, strength, speed, etc. all change. What works at one scale may be a disaster at another. To orientate us, it will pay to understand how some of the more fundamental parameters change as dimensions are reduced.

If you think of force as being like a piston supplied with pressure, the transmitted force is proportional to the area of the piston. In other words, it’s assumed that the stress (force/area) transmitted through the body is to be maintained constant as the size of the body is reduced. Thus force = SL² (S is the applied stress, assumed constant). Hence the transmitted force is proportional to area or to L² where L is some characteristic length dimension. Thus forces for a constant stress or pressure get smaller as the length scale is reduced. For example, a stress of 10¹⁰ N/m² scales to 10^-8 N/nm², i.e., 10 nN/nm².

Example 1

You can easily push on a restrained 1.0 cm cube of a material weighing 1.0 gm by a force of 1.0 Newton. If you want to apply the same stress to a 1.0 nm cube of the same material, what force do you apply?

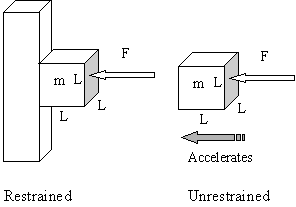
From the attached left hand figure, we can solve this using the scaling law we just noted.

In the macroscopic case, the stress is 1.0/(0.01 × 0.01) N/m² = 1.0 × 10⁴ N/m². In the nm case, the force is 1.0 × 10⁴ × (10^-9)² = 10^-14 N.

In this simple example it’s important to realize that our assumption of a constant stress is important. Had we decided that it’s more important to hold the acceleration of an unrestrained body constant (right figure) as we reduced the scale we would have gotten a different result. For example, to achieve the same acceleration on our nanometer body as on our 1.0 cm body, the necessary force is proportional to the mass of the respective cubes. In general the force = ma = ρVa (density × volume × acceleration) or F = ρL³a (the acceleration a is assumed constant).

In our example, the required force is 1.0 N × (10^-9/10^-2)³ = 10^-21 N (we just ratioed by the inverse cube of the length scale, L assuming the density of the material is uniform from the 1 cm scale all the way to the 1 nm scale).

Notice the stress scaling in the restrained body relates the force to the inverse square of the scaling length but the acceleration problem relates the force to the inverse cube of the scaling length. It comes down to judgment as to which is the appropriate model of the system. There is a factor of 10⁷ difference so it’s important!

Example 2

Suppose you had a pendulum weight suspended from a cable; if you doubled the size of everything, would the stress in the cable be the same, or more, or less than before? (This is a practical problem – how do they analyze cranes? Are large ones safe?)

If you look at the attached sketch with the original cube of side L and the cable of diameter D, and study the analysis presented there, it is clear that a system with all dimensions doubled would also double the stress in the support cable and it would have to be checked to determine if it was still safe!

K. Eric Drexler, “Nanosystems”, (John Wiley and Sons, NY, 1992), Chap. 2, suggests a number of macroscopically-based scaling laws some of which are summarized in the attached table.

Note some quantities in this table are invariant with length scaling, meaning they do not depend on a simple length scaling parameter at all. Thus, in this table, vibrations and speed do not depend on “L” (shorthand, “L⁰”) but paradoxically it appears that a characteristic time does depend linearly on “L”. By this statement is meant that if something typically will take 1 second to occur in a macroscopic system it is predicted to take 10^-9 seconds in a nanoscaled system.

The modeling of friction appears to be proportional to L², frictional heating to L², and wear life proportional to L. If these are physically realizable conclusions, friction^[2] is not going to worry us at the nano level, but wear lifetimes are. According to this table, something that has a lifetime of 1 year at the macroscopic level, might only have ~30 milliseconds at the nm scale! However, this desperate situation is dependent on a global model of friction that is not in accord with what we observe at the nano-level (as per Footnote 2) so it may not be as limiting as it appears.

From this table, and the physical assumptions behind it due to Drexler, we can now estimate speed scaling proportional to L⁰, i.e., invariant. So a 1 m/s speed translates to 1 m/s at the nanoscale and the time to traverse 1 nm is 1 nanosecond at 1 m/s.

Energy (or equally work) scales as force × distance, or proportional to L² × L, i.e., energy or work proportional to L³. Thus energy/work scales as volume. This is a large dependence since reducing scales by say 10⁸ reduces the energy or work by 10²⁴; however, we are often interested energy density or energy/unit volume and this is scale invariant. For example, if we can add 100 J to a 1 cubic centimeter block of material (energy density of 100 [J] × [100 cm/m]³ = 10⁸ J/m³) and apply the same energy density to a 10 nm cube, it should respond the same way. For example, if the 1 cm³ material is water, it will heat about ~24°C. The 10 nm cube will absorb 10⁸ J/m³ × (10 × 10^-9)³ = 10^-16 Joules. This will be heated through the same ~ 24°C provided the local 10 nm region is governed by the same laws of heat absorption as is the 1 cm³ volume.

Related variables include mechanical power and power density. Mechanical power scales as force × speed or power proportional to L² × L⁰ i.e., L² and power density or power/volume proportional to 1/L.

A gearbox for a present day car might occupy ~1 ft³ in volume and transmit ~150 HP. This translates to ~ 4 × 10⁶ W/m³ and thus transfers 4 × 10^-21 W per nm cube. However, if you could make a system work with 1 nN force operating at 1 m/s in a 1 nm cube (in a “MEMS”^[3] device for example), it will have a mechanical power density of 10⁺¹⁸ W/m³, an exceedingly high power density that far exceeds anything possible in macroscopic systems.

While the conclusions are based on laws of behavior that are not necessarily valid at small scales, these proposed mechanical scaling laws are particularly applicable to one major thrust area in nanotechnology – the manufacture of MEMS.