CVD and the Gas Laws

Chemical vapor deposition has requirements that are almost diametrically opposed to those for MBE. A modern prime example of CVD is the deposition of thin diamond films from the decomposition of a mixture of hydrogen and methane (CH₄, a.k.a. “natural gas” is what you burn in your home furnace in winter to keep warm). The resulting diamond material is usually in the form of intermeshed small diamond crystallites bound together into a thin sheet. This form of diamond has many potential electronic applications that include: 1) heat sinks for highly heat stressed^[1] diodes and 2) using diamond itself as a high temperature semiconductor for special severe applications. Another use of diamond sheets is to make long lasting cutting edges for machine tools, drill bits, medical scalpels etc. Such sheets usually consist of polycrystalline diamond of thickness of 100 – 400 μm for heat sinks and cutting tools but much thinner for possible future electronic applications.

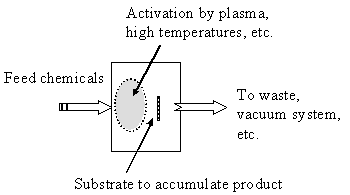
Whereas in MBE we did not want the gases in the molecular beams to interact until they impinged on the surface, we have to encourage interactions in CVD systems. A typical CVD system is shown in the inset figure; CVD systems normally operate at moderate vacuum or even at atmospheric pressure (say from ~ 10² Pa to 10⁵ Pa). Chemical decomposition of the feed molecules proceeds upstream of a target surface upon which you hope to trap the desired product. The chemistry is activated by high temperatures or by other means such as a “plasma”.

Plasma is a distinct state of matter in which the molecular or submolecular gaseous fragments gain positive charges that are offset by an intermingled cloud of electrons with their offsetting negative charges. Plasmas may contain positive ions and negative electrons as well as neutral atoms or molecules (or radical fractions thereof). Plasmas are most familiar as neon displays and in fluorescent lamps.

In many types of plasma, uncharged submolecular radicals are particularly important since they have highly reactive unpaired electrons from broken bonds just waiting to re-bond. These radicals are ready to form stable covalent^[2] bonds with other species. CVD methods mostly depend on the interaction of these gas phase radicals in order to chemically bond to the target substrate.

To better understand the conditions necessary for CVD we will digress into the mechanism that controls the CVD method of producing diamond films.

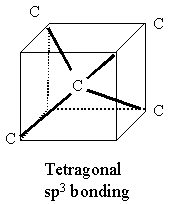
Diamonds contain repeats of sp³ bonds as per the insert figure. Each C atom lies in a tetragon with respect to its nearest neighbors. This is a very stable configuration and is responsible for the extreme rigidity of a diamond lattice when the pattern is repeated in bulk.

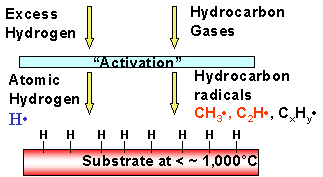
In order to produce diamonds from CH₄ and H₂ it requires that the hydrogen be “activated”. This is simply a convenient term that says, “H₂ gas is decomposed and produces H• radicals (the symbol • is to represent the fact we have an unpaired electron that would like to share with another to become stable). In a gaseous mixture of H• and CH₄, the H• radicals can interact with CH₄ producing CH₃•, i.e., so-called “methyl” radicals. To accomplish this, it is necessary that there be gaseous collisions between H• radicals and CH₄ molecules. This means that the CVD system pressure should not be too low.

Once formed, the CH₃• radical is an interesting species because it has a tetragonal structure that duplicates that of the diamond crystal. The figure below shows the probable instrumental reaction in forming the next diamond layer on top of a smaller fragment of diamond.

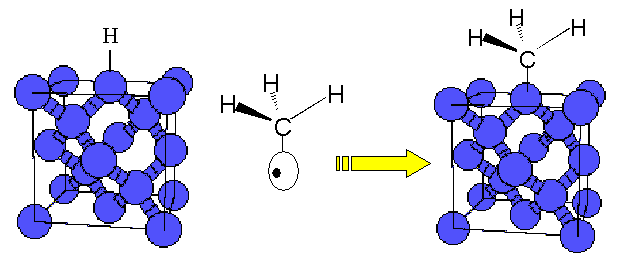
The diamond structure^[3] is shown with the blue spheres representing the individual carbon atoms. The white oblongs with the black nucleus is a representation of an electron orbital with one electron. To form a covalent bond, two of these electrons must get together and fill the orbital. Sufficient repeats of this process will form the next C layer with a repeat of the diamond C-C bond structure.

Why is hydrogen needed? At low pressure conditions (as in CVD), the thermodynamically stable carbon structure is not diamond but common graphite (as found in lead pencils). An hydrogen atoms is shown on the surface of the diamond (actually there is a full monolayer of H atoms). These hydrogen atoms are necessary to stabilize the deposited diamond so it does not form graphite. Vapor phase methyl radicals will form C-C bonds at hydrogenated sites on the diamond surface. Since the newly attached methyl radical is pre-hydrogenated, it is therefore protected against immediate graphitization. At temperatures of about 1,000°C, the protective hydrogen layer is lost from the surface and you can no longer make diamond; instead graphite is formed. This is obviously a measure of the strength of the H – C surface bond (see the module on Scaling Laws for a discussion of bond strength).

Thus the key to CVD diamond is the production of methyl radicals from methane; this occurs in the vapor phase by reversible binary chemical reactions such as:

To have this reaction occur in the gaseous phase, the gas pressure must be sufficient to have collisions (and possibly multiple collisions) between H• radicals and CH₄ molecules. The conceptual picture for the experimental self-assembly of diamond films is therefore as per the inset diagram.

Our previous plot of Knudsen number vs. system pressure is useful in determining some of the necessary (but not necessarily sufficient) requirements for this concept; the graph shows that the Knudsen number, λ/D, is at least < ~ 0.1 for p > ~ 5 Pa; this says that intermolecular collisions will occur ten times more than leakage to the walls of the reactor (i.e., just as desired). The pressure must be >~ 5 Pa by this criterion. To further emphasize multiple intermolecular collisions compared to the container walls, the criterion λ/D ~ 0.01 is probably a better call implying a reactor pressure of ~80 Pa.

But is this the most restrictive criterion? What about the reaction rate for these species? The volumetric collision rate given by

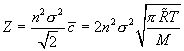
is an upper measure of the rate of production of methyl radicals that assumes all binary collisions are 1) 100% effective in producing methyl radicals and, more importantly, 2) that their concentration is given by n, the total number of particles in the space, whereas only a small fraction of hydrogen is its radical form.

The term Z/n is the fractional rate of binary collisions (since n is the total particles present per volume and Z/n = [collisions/m³/s] ÷ [particles/m³] = [collision/s/particle]. We need to compare this to the time available for gaseous reactions. We will further assume the residence time, τ, of the gaseous feed mixture in the reactor is 100 ms; in practice, this is simply given by the details of the flow rate and overall vessel volume. The probability of binary collisions is τZ/n.

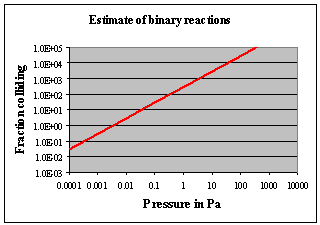
The result of the τZ/n calculation is given in the inset diagram at an assumed “activation” temperature of 2,000K; thus 100% of binary collisions should occur at a pressure of about 0.01 Pa and above. Since only a very small fraction of these collisions are likely to be effective (given the energetics of the reaction will also allow the reverse reaction to occur) it is prudent to allow large multiples of this estimate by increasing the working pressure well beyond the calculated 0.01 Pa. The previous criterion suggested that the pressure should be at least the previously estimated 80 Pa since at this pressures there will be about 10,000 collisions per particle in the reactor given 100 ms residence time there. Given the uncertainty in the concentration of H• radicals, this is a good place to start looking.

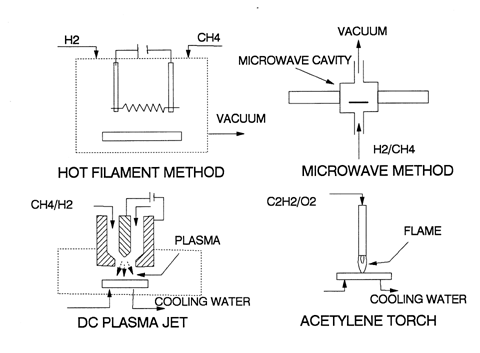
In fact diamond film growth has been reported from pressures of 100 Pa to 10⁵ Pa and typically 10³ Pa, thus confirming our basic assumptions. Various methods, all of relatively limited complexity compared to MBE, have been used and are summarized in the accompanying schematics.

The so-called hot filament approach is rather like an incandescent light bulb with H₂ and CH₄ flowing thorough it. A tungsten filament is maintained at a high temperature of about 2,500K (same as a familiar filament light bulb). A suitable substrate must be provided to capture the product; in general you do not need an epitaxial seed to deposit diamond in this way. The microwave and plasma jet methods are similar except they produce a higher concentration of initial H• than a hot filament and thus deposit more diamond at a faster rate.

Perhaps the most unlikely method to produce CVD diamond is a common acetylene welding torch. The flame is hot enough to produce H• and, in turn at atmospheric pressure, this produces both CH₃• and C₂H• radicals; the latter radicals may also directly deposit in a sp³ tetragonal orientation. In suitable microwave or plasma jets deposition rates as high as 1 mm/hr have been reported.

In summary: Chemical vapor deposition can work wonders in growing materials of many structures but:

• Relatively inexpensive equipment
• Usually, but not necessarily, using a modest vacuum system
• Capable of relatively high rates and specificity to 1000 μm/hr (mm/hr)
• Many commercial and research uses: superconductors, ceramics, hard materials, optical coatings, thermal barrier coatings, etc.