MBE and the Gas Laws

For the molecules or atoms in a molecular beam to strike the target surface and not be scattered out of the beam, we need to minimize the number of collisions among them; this means that we need a large mean free path at the beam conditions. This term is heavily influenced by pressure. The expression for the mean free path given previously is helpful in deciding whether gases molecules will collide with each other or, if they fail to do that, collide with their containment vessel’s walls. If the characteristic distance^[1] of the path for the gaseous molecules in the vacuum vessel is “D” a convenient parameter is λ/D. This parameter is called the “Knudsen” number whose physical significance is such that λ/D = 1 designates equal probability of two gas molecules colliding with each other or first reaching the vessel wall. If λ/D << 1 most collisions occur between gaseous molecules rather than with solid surfaces in the reactor. On the other hand if λ/D >> 1 there are relatively few intermolecular collisions and molecules will ballistically interact with surfaces in a direct line with the beam. In most MBE vessels, the walls are very cold effectively trapping the molecules as a condensed phase if they hit the walls of the vessel.

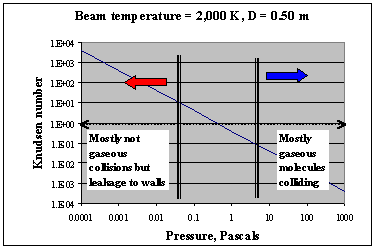
In the attached diagram, the pressure unit we have chosen is the standard SI unit of pascals (symbol “Pa” º 1 N/m²). One standard atmosphere is 100,000 Pa (i.e., 100,000 apples on a 1 meter square tray!). In the example plotted, λ/D ~ 1 occurs at a pressure of ~ 0.5 Pa so that we are probably in non-interactive zone if the pressure is less than about 0.05 Pa and in the interactive zone for a pressure of greater than ~ 5 Pa. Thus for MBE we would typically have to operate well below 0.05 Pa to ensure that the gas molecules arrived in their preferred state (e.g., as elemental Ga, Al or As etc. atoms). This vacuum is fairly readily accomplished using modern vacuum technology. But is this criterion sufficiently rigorous?

There is another factor we need to consider: how long will a clear surface remain clean if exposed to the background gas in a MBE reactor? The conservative calculation is to assume that every strike by gaseous atoms or molecules on the surface of the substrate target results in a contaminant atom or molecule that sticks to the surface. Of course the molecular beam is directed at a particular surface with the intent to stick atoms there, but background gas containing a small amount of air or water vapor (even high vacuum systems have small but inevitable leaks) represents an unwanted parallel path. To calculate the effect of such contaminants, we use the Hertz-Knudsen equation,

impingements/m² s, to estimate the rate of impingement of the background gas as a function of its pressure. If we assume that every impinging atom or molecule will stick to the surface, the inset graph is the result of that calculation assuming that the surface will be 100% coated at a density of 5 × 10¹⁸ atoms/m².

As the reactor vessel’s pressure falls from 10,000 Pa (i.e., 1/10 of atmospheric pressure) to 10^-6 Pa (10^-11 of atmospheric), the target surface will remain clean from ~10^-8 s to ~100 s respectively. Here “clean” is freedom from adventitious contaminant atoms or molecules originally present in the reactor’s gas space. If we presume we need to maintain our surfaces clean for 1 second or more, we will need system pressures of less than 10^-4 Pa, which is essentially where MBE is conducted.

But why pick 1 second? Exactly what the “clean time” should be associated with is the ability to switch the shutters for the effusion ovens that determine the overall composition of the molecular beam. Epitaxial growth rates are typically on the order of one nm/s or less “and the beams can be shuttered in a fraction of a second, allowing for nearly atomically abrupt transitions from one material to another^[2]”

The minimum time the surface remains clean probably is therefore a more restrictive criterion than the Knudsen number arguments given previously. This makes for the expensive and difficult equipment that is associated with MBE.

In summary: Molecular beam epitaxy can work wonders in growing prefect crystals in thin layers for electronics but:

• Expensive
• High vacuum
• Slow: Max ~ 1 – 5 atom/s or ~ 1 micrometer/hr (μm/hr)
• Homoepitaxy cannot grow outside of “seed” (i.e., target substrate)
• Heteroepitaxy needs imaginative “seeds”
• Slightly mismatched lattices cause fatal defects in product