Self-Assembly from the Gas Phase Exercises

A gas phase reactor is to deposit a self-assembled nano film from a mixture of reactive gases that is to be confined at 1,000K until there have been sufficient binary collisions among the gas molecules to ensure they are well equilibrated.

1. If there is a requirement that the number density of gaseous atoms, n, shall not exceed 10²⁰ atoms/m³ what is the corresponding gas pressure in Pa as given by the ideal gas law p = nkT?
   (Note: 1 pascal, Pa ≡ 1 N/m² & Boltzmann’s constant, k = 1.38 × 10^-23 J/K atom)

2. The binary collision frequency Z between colliding gas molecules is given by:

At the previously calculated condition if the collision diameter of these gas molecules is σ = 0.2 nm, N_Av = 6.022 × 10²⁶ atoms/ kg mole, & the molecular mass is M = 100 kg/kg. mole) find Z binary collisions/m³/s.

3. Interpret the expression Z/n in words implying why it may be useful.

Suggested Answers:

1. p = n kT = 10²⁰ [1/m³] × 1.38 × 10^-23 [J/K] × 1,000 [K] = 1.38 [J/m³] = 1.38 [N-m/m³] = 1.38 [N/m²] = 1.38 Pa
2. 
3. 
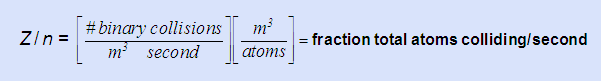
   tells you how long to wait to ensure complete equilibration. You probably would want to wait enough time for at least 10 – 100 times Z/n to ensure 100% effective collisions. In the above case residence time should be ~(10 – 100) × 10²⁰/7.34 × 10²³ = 1.4 – 14 milliseconds.

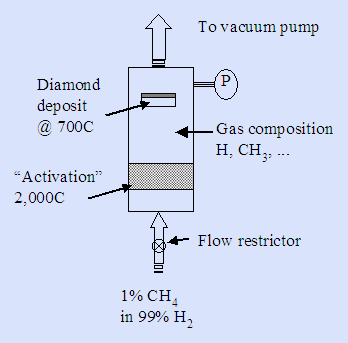
Here’s a part of a valid recipe from which you can make diamond starting from methane gas: 1% methane gas in 99% hydrogen gas is allowed to flow into a reaction chamber through a flow restrictor. The chamber pressure P, as recorded by the pressure gauge, is controlled by the dynamics of the restrictor and by a downstream vacuum pump that removes the excess materials.

Assume the reactor is 30 cm long by 10 cm diameter with a 5 cm diameter substrate. Your only job is to complete the reactor design.

1. First, what kind of bonding (covalent,van der Waals, or hydrogen) do you suspect can grow the diamond layers from methyl radicals?
2. It should have occurred to you need to fix the system pressure. Here are some suggestions (in nanobars, 1 bar = 1 normal unit of atmosphere): 1 nB, 10² nB, 10⁴ nB, 10⁶ nB, 10⁸ nB). Suggest and evaluate one or more gas-kinetic criteria that might be plausible for your purpose? (There might be a plausible range…)
3. Would you characterize this as a MBE system or a CVD system?

Suggested Answer

1. We are making the product at 700°C and apparently near to 100% of the bonds are happy at this temperature since this is a known method to grow diamond. This relatively high temperature should immediately suggest that there are pretty strong bonds involved. And, in fact they must be covalent to survive this temperature.

   If you assume the C-C covalent bond energy BE as 350 kJ/mol (which is about correct), you can estimate the stability of the bonding, by calculating the fraction of broken bonds from e^-BE/RT with T = 973K and 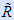= 8.314 J/mol K; this gives only ~ 1.6 × 10^-17 % broken bonds.

    

2. We need to decide how best to run this reactor; read the question statement for clues. Notice that the activation region provides big clues as to what is going on: hydrogen molecules are decomposed there. The resulting H• radicals apparently then attack CH₄, something they can only do if there are enough collisions between H• radicals and CH₄ molecules.

   Obviously we need gaseous interactions, not ballistic conditions (since the latter precludes collisions between gaseous atoms, radicals, molecules or other species). The best single criterion for collisions is the mean free path calculated from

                      

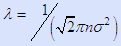
   in which n = p/kT and σ ~ 2 × 10^-10 m. The mean free path must be small compared to the reactor dimensions. It scales as the Knudsen number, K_n = λ/L where L is the equipment scaling dimension.

   We will have to guess at L from the problem statement. The reactor is 30 cm long by 10 cm diameter with a 5 cm diameter substrate. Obviously the reactor is not as big as a meter nor as small as a centimeter.

   If we guess that the length along the reactor flow path is important (since that is where collisions will occur before contacting the substrate) then L ~ 0.3 m is a crude guess – even though it may only be ~0.2 m or even less, 0.3 m is close enough for a quick guess. Hence we will need to use just one easy criterion:

   

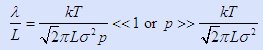
   You have also to pick a “system temperature” to plug into this equation. There is obviously a temperature gradient in our system from 2,000°C to 700°C. Use T ~ 1625K as an average.

   

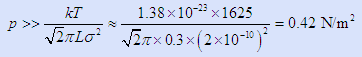
   (1 pascal = 1 N/m²)

   The approximations inherent in our guesses for both “T” and in “L” pale into insignificance compared to what we mean by “>>” (much greater than being the straightforward mathematical definition). We usually assume it means one order of magnitude, a factor of 10. Hence a defensible answer is that we need a pressure at least in excess of 4 Pa or 4 × 10⁴ nB.

   This is a fairly low pressure and in fact there is nothing stopping us from these gaseous considerations increasing this pressure; typical diamond growing in practice uses pressure of about 10⁶ – 10⁷ nB (this basically increases the maximum rate you can grow the stuff although with more and more defects, and this becomes mostly an economic criterion).

    

3. This is definitely a CVD system and not an MBE because there are more gas-to-gas collisions than gas-to-wall (using our Knudsen number criterion).